上周一数据结构上机,题目是”二叉树相关算法的实验验证”,其中要求
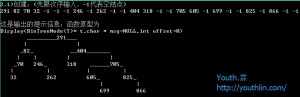
为便于观察程序的运行结果,设计的输出函数能在输出设备上以图形或表格或其它直观的形式输出计算结果。
例如将二叉树输出为1 / \ 2 3 / \ / \ 5 6 7 8
好吧,比较友好的让他显示树状就行了,可是想了很久就是不知道怎么办。。。上网搜索了一下”输出二叉树“,真正找到两篇有用的文章,一篇是CSDN copica博客的,一篇是中国知网的期刊论文(江顺亮,任燕)(我连论文都搜到了!!)
不过两篇都写的好复杂啊,copica君贴的代码太长了,看不太懂,我就把它打印下来了(这就是上一篇文章的作用…把网页选定的内容另存为pdf),顺便把知网那篇论文也下载了pdf一起打印出来。研究了一下结合两篇文章终于在上周六完成作业了哈哈~
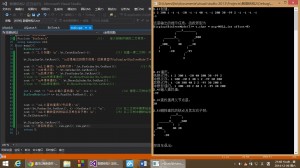
效果:
算法思路:
首先进行非递归的中根遍历,遍历过程中设置每个结点的坐标(即距离屏幕左边的偏移量offset),然后层次遍历根据坐标确定位置,因此需要给结点的struct增加几个数据域:
//结点声明
template<typename T> class BinTreeNode{
private:
BinTreeNode<T> *left, *right;//左右子树链接
T data;//数据域
int x = 0;//输出时的相对位置,在中根遍历时设置
int offset = -1;//距最左边的偏移量;即坐标。
int lw = -1;//左子宽度
int w = -1;//数据宽度
int rw = -1;//右子宽度
public:
//构造函数
BinTreeNode(const T& item, BinTreeNode<T> *lptr = NULL, BinTreeNode<T> *rptr = NULL) :data(item), left(lptr), right(rptr){}
BinTreeNode<T>* GetLeft(void)const { return left; } //返回左结点
void SetLeft(BinTreeNode<T>* l){ left = l; } //设置左结点
BinTreeNode<T>* GetRight(void) const{ return right; } //返回右结点
void SetRight(BinTreeNode<T>* r){ right = r; } //设置右结点
T& GetData(){ return data; } //返回数据域
void SetData(const T& item){ data = item; } //设置数据域
int& RgetX(){ return x; }
int& RgetOffset(){ return offset; }
int SetLw();
int GetLw();
int SetW();
int GetW();
int SetRw();
int GetRw();
//int DataWidth();
//设置数据域宽度
int DataWidth(int _data){
int len = 0;
(_data < 0) ? len = 1 : len = 0;//负数多个负号
do{
len++;
_data /= 10;
} while (_data);
return len;
}
int DataWidth(char _data){ return 1; }
int DataWidth(const char* _data){ return std::strlen(_data); }
int DataWidth(std::string _data){ return _data.length(); }
};
然后输出时层次遍历,使用队列打印每一层,因为我采用的输出方式是copica同学的方式,因此每层分为”连接符和数据+子树连接符竖线”,但copica的代码貌似使用了另一个print类来实现,因此我根据知网那篇论文还是用队列实现,程序中结点出队后又让他入队目的是打印”子树连接符”这一层,然后出队后就是子结点入队了,这个方法真巧妙~
以下贴出完整代码~~(点击方框右上在新窗口打开)
/*
第二次上机
题目:二叉树相关算法的实验验证
[实验目的]
验证二叉树的链接存储结构及其上的基本操作。
[实验内容及要求]
1、 定义链接存储的二叉树类。 √完成
2、 实验验证如下算法的正确性、各种功能及指标:
1)创建一棵二叉树,并对其初始化; √完成
2)先根、中根、后根遍历二叉树; √完成
3)在二叉树中搜索给定结点的父结点; √完成
4)搜索二叉树中符合数据域条件的结点; √完成
5)从二叉树中删除给定结点及其左右子树。 √完成
3、 为便于观察程序的运行结果,设计的输出函数能在输出设备上以图形或表格或其它直观的形式输出计算结果。 √完成!!
例如将二叉树输出为
1
/
2 3
/ /
5 6 7 8
4、 测试程序时,对所有输入变量取遍各种有代表性的值。 √完成
5、 为了增强程序的可读性,程序中要有适当的注释。 √完成
*/
#ifndef BINTREE_
#define BINTREE_
#include "AStack.h"
#include "AQueue.h"
#include <string>
using namespace std;
//AStack.h和AQueue.h还有本文件大部分代码都是教科书《数据结构》附录里的
//结点声明
template<typename T> class BinTreeNode{
private:
BinTreeNode<T> *left, *right; //左右子树链接
T data; //数据域
int x = 0; //输出时的相对位置,在中根遍历时设置
int offset = -1; //距最左边的偏移量;即坐标。
int lw = -1; //左子宽度
int w = -1; //数据宽度
int rw = -1; //右子宽度
public:
//构造函数
BinTreeNode(const T& item, BinTreeNode<T> *lptr = NULL, BinTreeNode<T> *rptr = NULL) :data(item), left(lptr), right(rptr){}
BinTreeNode<T>* GetLeft(void)const { return left; } //返回左结点
void SetLeft(BinTreeNode<T>* l){ left = l; } //设置左结点
BinTreeNode<T>* GetRight(void) const{ return right; } //返回右结点
void SetRight(BinTreeNode<T>* r){ right = r; } //设置右结点
T& GetData(){ return data; } //返回数据域
void SetData(const T& item){ data = item; } //设置数据域
int& RgetX(){ return x; }
int& RgetOffset(){ return offset; }
int SetLw();
int GetLw();
int SetW();
int GetW();
int SetRw();
int GetRw();
//int DataWidth();
//设置数据域宽度
int DataWidth(int _data){
int len = 0;
(_data < 0) ? len = 1 : len = 0;//负数多个负号
do{
len++;
_data /= 10;
} while (_data);
return len;
}
int DataWidth(char _data){ return 1; }
int DataWidth(const char* _data){ return std::strlen(_data); }
int DataWidth(std::string _data){ return _data.length(); }
};
template<typename T> int BinTreeNode<T>::GetLw(){
if (lw == -1)lw = SetLw();
return lw;
}
template<typename T> int BinTreeNode<T>::SetLw(){
if (left != NULL){
// _a
// |
// _b
//|
//c
//a的左边宽度=b左+b+b右。但 b+b右 < 2 时应 取2
lw = (left->GetW() + left->GetRw()) > 2 ? (left->GetW() + left->GetRw()) : 2;
lw += left->GetLw();
}
else lw = 0;
return lw;
}
template<typename T> int BinTreeNode<T>::GetRw(){
if (rw == -1)rw = SetRw();
return rw;
}
template<typename T> int BinTreeNode<T>::SetRw(){
if (right != NULL){
// a_
// |
// b
//a右宽=b左+b+b右。但 b左+b <2 时应取2
rw = (right->GetLw() + right->GetW()) > 2 ? (right->GetLw() + right->GetW()) : 2;
rw += right->GetRw();
}
else rw = 0;
return rw;
}
template<typename T> int BinTreeNode<T>::GetW(){
if (w == -1)w = SetW();
return w;
}
template<typename T> int BinTreeNode<T>::SetW(){
w = DataWidth(data);
return w;
}
//1、 定义链接存储的二叉树类。
//二叉树类-连接存储结构
template<typename T> class BinTree{
private:
BinTreeNode<T> *root; //根节点
T stop; //构造二叉树时的输入结束符,即输入stop则停止输入
public:
BinTree(BinTreeNode<T> *t = NULL) :root(t){} //构造函数
virtual ~BinTree(){ Del(root); } //析构函数,删除整棵二叉树,Del()函数稍后定义
//在以t为根的树中搜索p的父节点
BinTreeNode<T>* Father(BinTreeNode<T> *t, BinTreeNode<T>* p);
//在以t为根节点的树中查找data域值为item的结点
BinTreeNode<T>* Find(BinTreeNode<T>* t, const T& item)const;
//删除t子树(包括t结点本身)
void DelSubtree (BinTreeNode<T> *t);
void Del (BinTreeNode<T> *t);
void PreOrder (BinTreeNode<T> *t)const; //先根遍历 并输出该树
void InOrder (BinTreeNode<T> *t)const; //中根遍历 并输出该树
void PostOrder (BinTreeNode<T> *t)const; //后根遍历 并输出该树
void LevelOrder (BinTreeNode<T> *t)const; //层次遍历 并输出该树
void NorecPreOrder (BinTreeNode<T> *t)const; //非递归先根遍历 并输出该树
void NorecInOrder (BinTreeNode<T> *t,const int out = 1)const; //非递归中根遍历并计算中根序下各结点X坐标,如果out为真则输出该树
void NorecPostOrder (BinTreeNode<T> *t)const; //非递归后跟遍历 并输出该树
void SetX(){ NorecInOrder(root, 0); }
void CreatBinTree(T tostop); //创建二叉树
BinTreeNode<T>* Creat();
BinTreeNode<T>* CopyTree(BinTreeNode<T> *t); //复制二叉树t
//输出二叉树!
void Display(BinTreeNode<T> *t, //要输出的树
const char * msg = NULL, //msg:可选的提示信息,(应以结尾(用cout不需要也可以))
const int offset = 0); //offset:可选整体偏移量,
//其他操作
BinTreeNode<T> * GetRoot(){ return root; }
void SetRoot(BinTreeNode<T>* t){ root = t; }
T GetStop(){ return stop; }
void SetStop(T tostop){ stop = tostop; }
int IsEmpty(){ return root == NULL ? 1 : 0; }
};
//中根遍历-非递归
template<typename T> void BinTree<T>::NorecInOrder(BinTreeNode<T> *t, const int out = 1)const{
if (t == NULL)return;
t->SetLw(); t->SetW(); t->SetRw();
AStack<BinTreeNode<T>*> s;
int i = 0, z = 0;
BinTreeNode<T>* p = t;
while (p->GetLeft() != NULL){ p = p->GetLeft(); }
while (t != NULL || !s.IsEmpty()){
while (t != NULL){
s.Push(t);
t = t->GetLeft();
}
if (s.IsEmpty())return;
i++;
s.Pop(t);
if (p == t){ t->RgetOffset() = 0; }//第一个结点
else{
if (t->GetLeft() == p){//t是前一个节点p的父结点
/*
* _2 __1
*| |
*1 100
*/
z = p->GetW();
if (z < 2)z = 2;
t->RgetOffset() = p->RgetOffset() + z;
//cout << p->RgetOffset() << "(p.o)" << p->GetW() << "(p.W) " << z << "n";
}
else if (p->GetRight() == t){//t是前一个节点p的子节点
/*
*012 01234
*2_ 200_
* | |
* 3 233
*/
t->RgetOffset() = p->RgetOffset() + p->GetW() + 1;
}
else{//t和前一个结点p不是父子关系
/*
* ____1 100___
*| |
*3_ __3
* | |
* 200 200
*/
t->RgetOffset() = p->RgetOffset() + p->GetW();
}
p = t;
//cout << p->RgetOffset() << ") ";
}//t不是第一个结点
if (out){ std::cout << t->GetData() << " "; }
t->RgetX() = i;
t = t->GetRight();
}
}
//层次遍历 (使用了队列AQueue类)
template<typename T> void BinTree<T>::LevelOrder(BinTreeNode<T> *t)const{
/*
//书上的,一次全部输出
if (t == NULL)return;
BinTreeNode<T> *p;
AQueue<BinTreeNode<T>*> q;
q.QInsert(t);
while (!q.isEmpty()){
q.QDelete(p);
std::cout << p->GetData() << " ";
if (p->GetLeft() != NULL)q.QInsert(p->GetLeft());
if (p->GetRight() != NULL)q.QInsert(p->GetRight());
}
*/
if (t == NULL)return;
BinTreeNode<T> *p = t, *end = new BinTreeNode<T>(stop);
AQueue<BinTreeNode<T>*> q;
q.QInsert(p);
q.QInsert(end);
while (true)
{
q.QDelete(p);
if (q.isEmpty())break;
if (p != end){ std::cout << p->GetData() << " "; }
else { std::cout << "n"; q.QInsert(end); }
if (p->GetLeft() != NULL){ q.QInsert(p->GetLeft()); }
if (p->GetRight() != NULL){ q.QInsert(p->GetRight()); }
}
std::cout << "n";
delete p;
//delete end;
}
//输出二叉树!!
template<typename T> void BinTree<T>::Display(BinTreeNode<T> * t, const char * msg, const int offset){
if (msg){ cout << msg << "n"; }
//cout << "DDDDDDDDDDDDDDDDDDDDDDDDDDDDn";//////////////////////////////////////////////////////////////
if (NULL == t)return;
NorecInOrder(t, 0);//设置每个结点的宽度、坐标。
BinTreeNode<T> *p = t, *end = new BinTreeNode<T>(stop);
AQueue<BinTreeNode<T>*> q;
q.QInsert(p); q.QInsert(end);
int j=0;//光标的当前坐标
for (int i = 0; i < offset; i++){ cout << " "; }
while (true)
{
if (q.QFront() == end){ cout << "n"; break; }
//数据层
while (true)
{
q.QDelete(p);
q.QInsert(p);
//cout << p->GetData() << "(data)n";
if (p == end){
cout << "n";
for (int i = 0; i < offset; i++){ cout << " "; }
j = 0;
break; }
if (p->GetLeft() != NULL){
for (; j <= p->GetLeft()->RgetOffset(); j++){ cout << " "; }
for (; j < p->RgetOffset(); j++){ cout << "_"; }
}
else{
for (; j < p->RgetOffset(); j++){ cout << " "; }
}
cout << p->GetData(); j += p->GetW();
if (p->GetRight() != NULL){
for (; j < p->GetRight()->RgetOffset(); j++){ cout << "_"; }
}
}//数据层
//“|”连接层
while (true)
{
q.QDelete(p);
if (p == end){
cout << "n";
for (int i = 0; i < offset; i++){ cout << " "; }
j = 0;
q.QInsert(end);
break;
}
if (p->GetLeft() != NULL){
for (; j < p->GetLeft()->RgetOffset(); j++){ cout << " "; }
cout << "|"; j++;//半角管道符
//cout << "│"; j+=3;//全角制表符-不好控制
q.QInsert(p->GetLeft()); }
if (p->GetRight() != NULL){
for (; j < p->GetRight()->RgetOffset(); j++){ cout << " "; }
cout << "|"; j++;//半角管道符
//cout << "│"; j+=3;//全角制表符-不好控制
q.QInsert(p->GetRight());
}
}//连接层
}//层次遍历输出
}//void
//1)创建一棵二叉树,并对其初始化;
//调用时必须指明tostop值,然后本函数调用Creat。
template<typename T> void BinTree<T>::CreatBinTree(T tostop){
SetStop(tostop);
root = Creat();
}
//数据在这个函数输入,以设置的stop代替空结点,先根次序输入。
template<typename T> BinTreeNode<T>* BinTree<T>::Creat(){
BinTreeNode<T> *t, *t1, *t2;
T item;
cin >> item;
if (item == stop){ t = NULL; return t; }
else{
if (!(t = new BinTreeNode<T>(item, NULL, NULL)))return NULL;
t1 = Creat();
t->SetLeft(t1);
t2 = Creat();
t->SetRight(t2);
return t;
}
}
//2)先根、中根、后根遍历二叉树;
//先根遍历-递归
template<typename T> void BinTree<T>::PreOrder(BinTreeNode<T> *t)const{
if (t != NULL){
std::cout << t->GetData() <<" ";
PreOrder(t->GetLeft());
PreOrder(t->GetRight());
}
}
//中根遍历-递归
template<typename T> void BinTree<T>::InOrder(BinTreeNode<T> *t)const{
if (t != NULL){
InOrder(t->GetLeft());
std::cout << t->GetData() << " ";
InOrder(t->GetRight());
}
}
//后根遍历-递归
template<typename T> void BinTree<T>::PostOrder(BinTreeNode<T> *t)const{
if (t != NULL){
PostOrder(t->GetLeft());
PostOrder(t->GetRight());
std::cout << t->GetData() <<" ";
}
}
//3)在二叉树中搜索给定结点的父结点;
template<typename T> BinTreeNode<T>* BinTree<T>::Father(BinTreeNode<T>* t, BinTreeNode<T>* p){
BinTreeNode<T> *q;
if (t == NULL || p == NULL)return NULL; //若其中之一为空返回空
if (t->GetLeft() == p || t->GetRight() == p)return t; //若t即为p父节点,直接返回t
//在左右子树中寻找(递归)
if ((q = Father(t->GetLeft(), p)) != NULL)return q;
else return Father(t->GetRight(), p);
}
//4)搜索二叉树中符合数据域条件的结点;
template<typename T> BinTreeNode<T> * BinTree<T>::Find(BinTreeNode<T> *t, const T& item)const{
BinTreeNode<T> *p, *q;
if (NULL == t)return NULL;
if (t->GetData() == item)return t;
if ((p = Find(t->GetLeft(), item)) != NULL)return p;
else return q = Find(t->GetRight(), item);
}
//5)从二叉树中删除给定结点及其左右子树。
//删除子树t
//需要用到Father(),Del(),BinTreeNode.
template<typename T> void BinTree<T>::DelSubtree(BinTreeNode<T>* t){
if (NULL == t)return;
if (t == root){
Del(t);
root = NULL;
return;
}
BinTreeNode<T> *p, *q;
p = t;
q = Father(root, p);
if (q){
if (q->GetLeft() == p)q->SetLeft(NULL);
if (q->GetRight() == p)q->SetRight(NULL);
}
Del(p);
}
//删除树t
template<typename T> void BinTree<T>::Del(BinTreeNode<T>* t){
if (t != NULL){
Del(t->GetLeft());
Del(t->GetRight());
delete t;
}
}
#endif
参考:
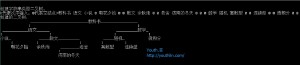
Update at 2016-06-18 22:49:37 多叉树的输出
声明
- 本作品采用署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。除非特别注明, 霖博客文章均为原创。
- 转载请保留本文(《二叉树的文本模式输出》)链接地址: https://youthlin.com/?p=868
- 订阅本站:https://youthlin.com/feed/
“二叉树的文本模式输出”上的29条回复
[…] 之前做课程设计时写过二叉树的输出,最近,写 SNL 语言的编译程序的语法分析器,需要输出语法树,而语法树是多叉树,与二叉树的输出有点不一样。 […]
看到代码我头都大了。
理论性很强
文章写得可能有点乱,当初是只是记录下来给自己看的,其他人看可能会有点费劲
程序员中的技术帝。
程序员还算不上,技术帝跟不敢当
二叉树 不知道这玩意
名字有些独特。二叉树。
我能看懂,哈
历史君文理工三全哈哈
//我觉得有必要添加几个表情(如‘ [/抱拳] ’)了
技术帝就是厉害
好吧好吧,我不会告诉你我看不懂的
我也对这些代码一窍不通啊
对这些代码一窍不通啊
太专业了,没接触过这方面。
nice
不错
程序员的技术博客必须的顶一顶
我也跟着楼上倒。![[/撇嘴]](https://youthlin.com/wp-content/themes/twentytwenty-child/images/smilies/撇嘴.gif)
还是没懂输出时有层次结构是怎么记录哪个层哪个叶的。
遍历倒是有点思路,4月份的时候试过一个,我的遍历在我这篇:http://xcy.me/e/21260
学习的态度相当的认真。
去开发单片机,有前途一点
我一点都不想再学有关硬件的东西了,模电和计算机组成原理已学死
现在还没睡
好难看得懂的代码。
这是以后要往C/C艹发展的吗。。。
可能不会吧,只是现在只学了C/C艹 下学期JAVA
这个玩意得作用是??
没什么作用,数据结构上机作业。。。
已晕![[/流泪]](https://youthlin.com/wp-content/themes/twentytwenty-child/images/smilies/流泪.gif)